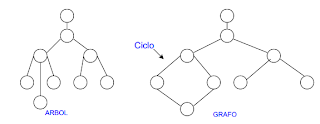
Arboles.
Definición
Un árbol es una
estructura de datos dinámica (las estructuras del árbol pueden cambiar durante
la ejecución del programa) no lineal (puesto que a cada elemento del árbol
puede seguirle varios elementos) y homogénea en el que cada elemento puede
tener varios elementos posteriores y solamente un elemento anterior. Es una
estructura jerárquica aplicada sobre una colección de elementos u objetos
llamados nodos, de los cuales uno es conocido como raíz, además se crea una
relación de parentesco entre los nodos dando lugar a términos como padre,
hijo, hermano, antecesor, sucesor, ancestro, etc.
Clasificación.
Distintos: Dos árboles binarios son
distintos cuando sus estructuras son diferentes.
Similares: Dos árboles binarios son
similares cuando sus estructuras son idénticas, pero la información que
contienen sus nodos es diferente.
Equivalentes: Son aquellos árboles que son
similares y que además los nodos contienen la misma información.
Completos: Son aquellos árboles en los que
todos sus nodos excepto los del último nivel, tiene dos hijos; subárbol
izquierdo y el subárbol derecho.
Árbol binario
Representación
Grafica
Representación en memoria.
Hay dos formas
tradicionales de representar un árbol binario en memoria:
1.-Por medio de
datos tipo punteros también conocidos como variables dinámicas o listas. Esta
es la forma más utilizada, puesto que es la más natural para tratar este tipo
de estructuras.
2.-Por medio de
arreglos. Los nodos del árbol binario serán representados como registros que
contendrán como mínimo tres campos. En un campo se almacenará la información
del nodo. Los dos restantes se utilizarán para apuntar al subárbol izquierdo y
derecho del subárbol en cuestión.
Aplicaciones:
Las aplicaciones de
los arboles binarios se les puede utilizar para representar una estructura en
la cual es posible tomar decisiones con dos opciones en distintos puntos.
Una aplicación de
los árboles binarios es la de representar una expresión que contiene operando y
operadores binarios.
Una aplicación de
los árboles binarios es la creación de Árboles binarios de búsqueda, en donde
dada una secuencia de datos el árbol binario de búsqueda se construye dadas las
sig. reglas:
·
Cualquier
nodo del subárbol derecho contiene Información >= al nodo padre.
·
Cualquier
nodo del subárbol izquierdo contiene Información < al nodo padre.
Diferencias
entre un árbol general y un árbol binario:
Son árboles cuyo
grado es mayor que dos.
Por cada nodo: la
información y una lista de referencia saca da uno de sus hijos.
•Secuencial: Se
pierde espacio, cada nodo tiene un agrado diferente.
•Enlazada: la manipulación
de la lista de hijos se hace difícil.
Bibliografías:
http://blog.unab.cl/maxbecerrabustamante/arboles/
http://upload.wikimedia.org/wikipedia/commons/5/51/APUNTES.pdf
http://es.scribd.com/doc/24062352/Arboles-y-Grafos
http://www.slideshare.net/ulises_e/savedfiles?s_title=arboles-1670628&user_login=zamanthag