GRAFOS
Un grafo está formado por un conjunto de nodos(o vértices) y un conjunto de arcos. Cada arco en un grafo se especifica por un par de nodos.
El conjunto de nodos es {A, B, C, D, F, G, H} y el conjunto de arcos {(A, B), (A, D), (A,
C), (C, D), (C, F), (E, G), (A, A)} para el siguiente grafo:
Si los pares de nodos en los arcos dirigidos, el grafo se denomina grafo directo, dirigido o dígrafo.
Terminología.
- Vértice: Nodo
- Enlace: Conexión entre dos vértices (nodos).
- Adyacencia : Se dice que dos vértices son adyacentes si entre ellos hay un enlace directo.
- Vecindad: Conjunto de vértices adyacentes a otro.
- Camino: Conjunto de vértices que hay que recorrer para llegar desde un nodo origen hasta un nodo destino.
- Grafo conectado: Aquél que tiene camino directo entre todos los nodos.
- Grafo dirigido: Aquél cuyos enlaces son unidireccionales e indican hacia donde están dirigidos.
- Gafo con pesos: Aquél cuyos enlaces tienen asociado un valor. En general en este tipo de grafos no suele tener sentido que un nodo se apunte a sí mismo porque el coste de este enlace sería nulo.
Matriz de adyacencia.
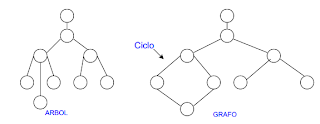
.-Un grafo sin ciclos es un árbol.
*.-El entregado de un nodo indica el número de arcos que llegan a ser nodo.
*.-El fuera de grado de un nodo indica el número de arcos que salen de él.
*.-Un grafo de N vértices o nodos es un árbol si cumple las siguientes condiciones
a) Tiene N-1 arcos
b) Existe una trayectoria entre cada par de nodos.
c) Esta mínimamente conectado.
*.-Un grafo esta etiquetado si sus arcos tiene valores asignados. Si este valor es numérico
se dice que el grafo tiene peso.
Recorrido de un grafo:
Hay dos tipos de recorridos de un grafo, y pueden ser implementados tanto de forma recursiva como de forma iterativa. Estos recorridos son:
- En profundidad, que consiste en alejarse todo lo posible del nodo origen para después empezar a visitar los nodos restantes a la vuelta.
- A lo ancho (o por nivel), que consiste en visitar primero los nodos vecinos del origen, luego los vecinos de éstos, y así sucesivamente.
Bibliografía:
- http://profesores.elo.utfsm.cl/~tarredondo/info/datos-algoritmos/ELO-320%20Grafos.pdf
- http://www.itnuevolaredo.edu.mx/takeyas/Apuntes/Estructura%20de%20Datos/Apuntes/grafos/Apuntes_Grafos.pdf
- http://www.iuma.ulpgc.es/users/jmiranda/docencia/programacion/Tema9_ne.pdf



No hay comentarios:
Publicar un comentario